Quickstart¶
Defining the orbit: Orbit objects¶
The core of hapsira are the Orbit objects inside the hapsira.twobody module. They store all the required information to define an orbit:
The body acting as the central body of the orbit, for example the Earth.
The position and velocity vectors or the orbital elements.
The time at which the orbit is defined.
First of all, you have to import the relevant modules and classes:
from astropy import units as u
from hapsira.bodies import Earth, Mars, Sun
from hapsira.twobody import Orbit
From position and velocity¶
There are several methods available to create Orbit objects. For example, if you have the position and velocity vectors you can use from_vectors():
# Data from Curtis, example 4.3
r = [-6045, -3490, 2500] << u.km
v = [-3.457, 6.618, 2.533] << u.km / u.s
orb = Orbit.from_vectors(Earth, r, v)
And that’s it! Notice a couple of things:
Defining vectorial physical quantities using Astropy units is very easy. The list is automatically converted to a
astropy.units.Quantity, which is actually a subclass of NumPy arrays.If you display the orbit you just created, you get a string with the radius of pericenter, radius of apocenter, inclination, reference frame and attractor:
>>> orb 7283 x 10293 km x 153.2 deg (GCRS) orbit around Earth (♁) at epoch J2000.000 (TT)
If no time is specified, then a default value is assigned:
>>> orb.epoch <Time object: scale='tt' format='jyear_str' value=J2000.000> >>> orb.epoch.iso '2000-01-01 12:00:00.000'
The reference frame of the orbit will be one pseudo-inertial frame around the attractor. You can retrieve it using the
frameproperty:>>> orb.get_frame() <GCRS Frame (obstime=J2000.000, obsgeoloc=(0., 0., 0.) m, obsgeovel=(0., 0., 0.) m / s)>
Intermezzo: quick visualization of the orbit¶
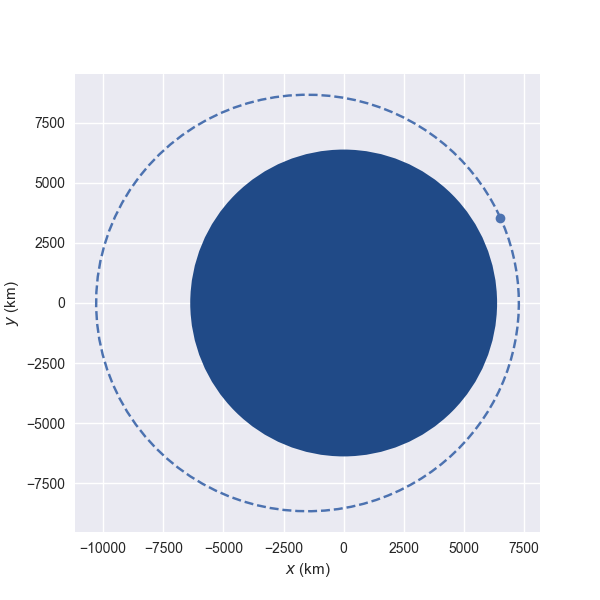
If you’re working on interactive mode (for example, using JupyterLab) you can immediately plot the current orbit:
orb.plot()
This plot is made in the so called perifocal frame, which means:
you’re visualizing the plane of the orbit itself,
the $(x)$ axis points to the pericenter, and
the $(y)$ axis is turned $90 \mathrm{^\circ}$ in the direction of the orbit.
The dotted line represents the osculating orbit: the instantaneous Keplerian orbit at that point. This is relevant in the context of perturbations, when the object shall deviate from its Keplerian orbit.
Note
This visualization uses Plotly under interactive environments like Jupyter Notebook or Jupyter Lab while it switches to Matplotlib otherwise. Nevertheless, you can select the drawing backend. Check out the hapsira.plotting.orbit.OrbitPlotter documentation for more information.
From classical orbital elements¶
You can also define an Orbit using a set of six parameters called orbital elements. Although there are several of these element sets, each one with its advantages and drawbacks, right now hapsira supports the classical orbital elements:
Semimajor axis $(a)$.
Eccentricity $(e)$.
Inclination $(i)$.
Right ascension of the ascending node $(\Omega)$.
Argument of pericenter $(\omega)$.
True anomaly $(\nu)$.
In this case, you’d use the method from_classical():
# Data for Mars at J2000 from JPL HORIZONS
a = 1.523679 << u.AU
ecc = 0.093315 << u.one
inc = 1.85 << u.deg
raan = 49.562 << u.deg
argp = 286.537 << u.deg
nu = 23.33 << u.deg
orb = Orbit.from_classical(Sun, a, ecc, inc, raan, argp, nu)
Notice that whether you create an Orbit from $(r)$ and $(v)$ or from elements you can access many mathematical properties of the orbit:
>>> orb.period.to(u.day)
<Quantity 686.9713888628166 d>
>>> orb.v
<Quantity [ 1.16420211, 26.29603612, 0.52229379] km / s>
To see a complete list of properties, check out the Orbit class on the API reference.
Moving forward in time: propagation¶
Now that you have defined an orbit, you might be interested in computing how is it going to evolve in the future. In the context of orbital mechanics, this process is known as propagation.
For example, start by importing an example orbit from the International Space Station:
>>> from hapsira.examples import iss
>>> iss
6772 x 6790 km x 51.6 deg (GCRS) orbit around Earth (♁)
>>> iss.epoch
<Time object: scale='utc' format='iso' value=2013-03-18 12:00:00.000>
>>> iss.nu.to(u.deg)
<Quantity 46.595804677061956 deg>
>>> iss.n.to(u.deg / u.min)
<Quantity 3.887010576192155 deg / min>
Using the propagate() method you can now retrieve the position of the ISS after some time:
>>> iss_30m = iss.propagate(30 << u.min)
>>> iss_30m.epoch # Notice you advanced the epoch!
<Time object: scale='utc' format='iso' value=2013-03-18 12:30:00.000>
>>> iss_30m.nu.to(u.deg)
<Quantity 163.1409357544868 deg>
To explore different propagation algorithms, check out the hapsira.twobody.propagation module.
Studying trajectories: Ephem objects¶
The propagate method gives you the final orbit at the epoch you designated. To retrieve the whole trajectory instead, you can use hapsira.twobody.orbit.scalar.Orbit.to_ephem(), which returns an Ephem instance:
from hapsira.twobody.sampling import EpochsArray, TrueAnomalyBounds, EpochBounds
from hapsira.util import time_range
start_date = Time("2022-07-11 05:05", scale="utc")
end_date = Time("2022-07-11 07:05", scale="utc")
# One full revolution
ephem1 = iss.to_ephem()
# Explicit times given
ephem2 = iss.to_ephem(strategy=EpochsArray(epochs=time_range(start_date, end_date)))
# Automatic grid, true anomaly limits
ephem3 = iss.to_ephem(strategy=TrueAnomalyBounds(min_nu=0 << u.deg, max_nu=180 << u.deg))
# Automatic grid, epoch limits
ephem4 = iss.to_ephem(strategy=EpochBounds(min_epoch=start_date, max_epoch=end_date))
Ephem objects contain the coordinates of an object sampled at specific times. You can access both:
>>> ephem1.epochs[:3]
<Time object: scale='utc' format='iso' value=['2013-03-18 12:23:55.155' '2013-03-18 12:24:51.237'
'2013-03-18 12:25:47.323']>
>>> ephem1.sample(ephem1.epochs[:3])
<CartesianRepresentation (x, y, z) in km
[( 859.07256 , -4137.20368 , 5295.56871 ),
(1270.55257535, -4012.16848983, 5309.55706958),
(1676.93829596, -3870.95571409, 5302.1480373 )]
(has differentials w.r.t.: 's')>
Studying non-keplerian orbits: perturbations¶
Apart from the Keplerian propagators, hapsira also allows you to define custom perturbation accelerations to study non Keplerian orbits, thanks to Cowell’s method:
>>> from numba import njit
>>> import numpy as np
>>> from hapsira.core.propagation import func_twobody
>>> from hapsira.twobody.propagation import CowellPropagator
>>> r0 = [-2384.46, 5729.01, 3050.46] << u.km
>>> v0 = [-7.36138, -2.98997, 1.64354] << (u.km / u.s)
>>> initial = Orbit.from_vectors(Earth, r0, v0)
>>> @njit
... def accel(t0, state, k):
... """Constant acceleration aligned with the velocity. """
... v_vec = state[3:]
... norm_v = (v_vec * v_vec).sum() ** 0.5
... return 1e-5 * v_vec / norm_v
...
... def f(t0, u_, k):
... du_kep = func_twobody(t0, u_, k)
... ax, ay, az = accel(t0, u_, k)
... du_ad = np.array([0, 0, 0, ax, ay, az])
... return du_kep + du_ad
>>> initial.propagate(3 << u.day, method=CowellPropagator(f=f))
18255 x 21848 km x 28.0 deg (GCRS) orbit around Earth (♁) at epoch J2000.008 (TT)
Some natural perturbations are available in hapsira to be used directly in this way. For instance, to examine the effect of J2 perturbation:
>>> from hapsira.core.perturbations import J2_perturbation
>>> tofs = [48.0] << u.h
>>> def f(t0, u_, k):
... du_kep = func_twobody(t0, u_, k)
... ax, ay, az = J2_perturbation(
... t0, u_, k, J2=Earth.J2.value, R=Earth.R.to(u.km).value
... )
... du_ad = np.array([0, 0, 0, ax, ay, az])
... return du_kep + du_ad
>>> final = initial.propagate(tofs, method=CowellPropagator(f=f))
The J2 perturbation changes the orbit parameters (from Curtis example 12.2):
>>> ((final.raan - initial.raan) / tofs).to(u.deg / u.h)
<Quantity -0.17232668 deg / h>
>>> ((final.argp - initial.argp) / tofs).to(u.deg / u.h)
<Quantity 0.28220397 deg / h>
Studying artificial perturbations: thrust¶
In addition to natural perturbations, hapsira also has built-in artificial perturbations (thrust guidance laws) aimed at intentional change of some orbital elements. For example, to simultaneously change eccentricity and inclination:
>>> ecc_0, ecc_f = [0.4, 0.0] << u.one
>>> a = 42164 << u.km
>>> inc_0 = 0.0 << u.deg # baseline
>>> inc_f = 20.0 << u.deg
>>> argp = 0.0 << u.deg # the method is efficient for 0 and 180
>>> f = 2.4e-7 << (u.km / u.s ** 2)
# Retrieve r and v from initial orbit
>>> orb0 = Orbit.from_classical(
... Earth,
... a,
... ecc_0,
... inc_0,
... 0,
... argp,
... 0,
... )
>>> a_d, _, t_f = change_ecc_inc(orb0, ecc_f, inc_f, f)
# Propagate orbit
>>> def f_geo(t0, u_, k):
... du_kep = func_twobody(t0, u_, k)
... ax, ay, az = a_d(t0, u_, k)
... du_ad = np.array([0, 0, 0, ax, ay, az])
... return du_kep + du_ad
>>> orbf = orb0.propagate(t_f << u.s, method=CowellPropagator(f=f_geo, rtol=1e-8))
The thrust changes orbit parameters as desired (within errors):
>>> orbf.inc, orbf.ecc
(<Quantity 0.34719734 rad>, <Quantity 0.00894513>)
For more available thrust guidance laws options, see the hapsira.twobody.thrust module.
Changing the orbit: Maneuver objects¶
hapsira helps defining several in-plane and general out-of-plane maneuvers with the Maneuver class.
Each Maneuver consists on a list of impulses $\Delta v_i$ (changes in velocity), each one applied at a certain instant $t_i$. The simplest maneuver is a single change of velocity without delay: you can recreate it either using the impulse() method or instantiating it directly.
from hapsira.maneuver import Maneuver
dv = [5, 0, 0] << (u.m / u.s)
imp = Maneuver.impulse(dv)
imp = Maneuver((0 << u.s, dv)) # Equivalent
There are other useful methods you can use to compute common in-plane maneuvers, notably {py:meth} ~hapsira.maneuver.Maneuver.hohmann and bielliptic() for Hohmann and bielliptic transfers respectively. Both return the corresponding Maneuver object, which in turn you can use to calculate the total cost in terms of velocity change $\sum |\Delta v_i|$ and the transfer time:
>>> orb_i = Orbit.circular(Earth, alt=700 << u.km)
>>> orb_i
7078 x 7078 km x 0.0 deg (GCRS) orbit around Earth (♁)
>>> hoh = Maneuver.hohmann(orb_i, 36000 << u.km)
>>> hoh.get_total_cost()
<Quantity 3.6173981270031357 km / s>
>>> hoh.get_total_time()
<Quantity 15729.741535747102 s>
You can also retrieve the individual vectorial impulses:
>>> hoh.impulses[0]
(<Quantity 0 s>, <Quantity [ 0. , 2.19739818, 0. ] km / s>)
>>> hoh[0] # Equivalent
(<Quantity 0 s>, <Quantity [ 0. , 2.19739818, 0. ] km / s>)
>>> tuple(val.decompose([u.km, u.s]) for val in hoh[1])
(<Quantity 15729.741535747102 s>, <Quantity [ 0. , 1.41999995, 0. ] km / s>)
To actually retrieve the resulting Orbit after performing a maneuver, use the method apply_maneuver():
>>> orb_f = orb_i.apply_maneuver(hoh)
>>> orb_f
36000 x 36000 km x 0.0 deg (GCRS) orbit around Earth (♁)
More advanced plotting: OrbitPlotter objects¶
You previously saw the plot() method to easily plot orbits. Now you might want to plot several orbits in one graph (for example, the maneuver you computed in the previous section). For this purpose, hapsira has an OrbitPlotter object in the plotting module.
The advantage of this object is that it allows you to select the desired drawing backend. All the supported backends are specified in the dictionary SUPPORTED_ORBIT_PLOTTER_BACKENDS.
If you would like to know which 2D check the SUPPORTED_ORBIT_PLOTTER_BACKENDS_2D. For 3D backends, refer to SUPPORTED_ORBIT_PLOTTER_BACKENDS_3D.
Note that some backends are interactive, meaning that you can move the scene or even rotate the three-dimensional view in a dynamic way.
To easily visualize several orbits in two dimensions, you can run this code:
from hapsira.plotting import OrbitPlotter
op = OrbitPlotter(backend_name="matplotlib2D")
orb_a, orb_f = orb_i.apply_maneuver(hoh, intermediate=True)
op.plot(orb_i, label="Initial orbit")
op.plot(orb_a, label="Transfer orbit")
op.plot(orb_f, label="Final orbit")
op.show()
which produces this beautiful plot:
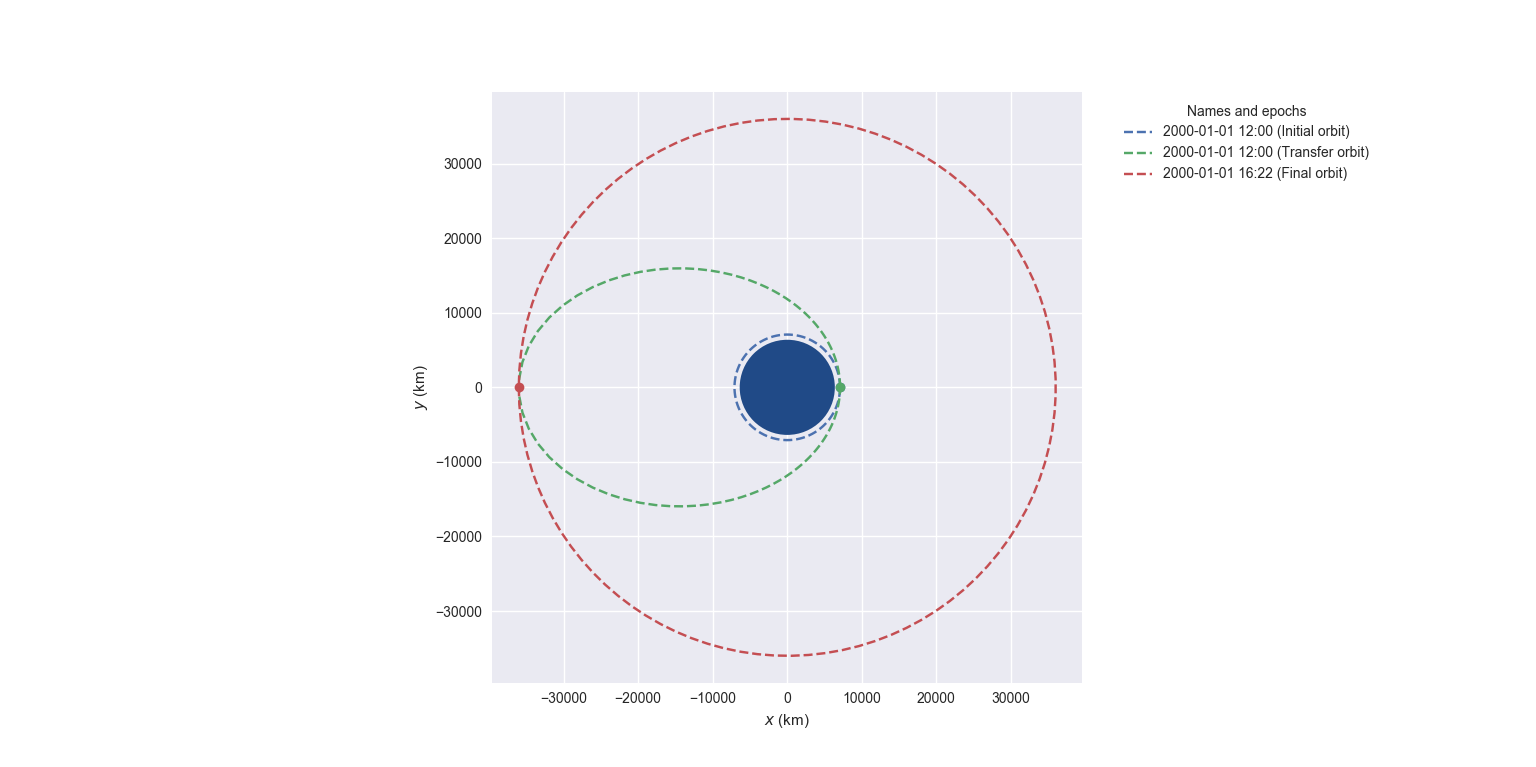
Plot of a Hohmann transfer.¶
Where are the planets? Computing celestial ephemerides¶
New in version 0.14.0.
Thanks to Astropy and jplephem, hapsira can read Satellite Planet Kernel (SPK) files, part of NASA’s SPICE toolkit. This means that you can query the position and velocity of the planets of the Solar system.
The hapsira.ephem.Ephem class allows you to retrieve a planetary orbit using low precision ephemerides available in Astropy:
>>> from astropy.time import Time
>>> epoch = time.Time("2020-04-29 10:43") # UTC by default
>>> from hapsira.ephem import Ephem
>>> earth = Ephem.from_body(Earth, epoch.tdb)
>>> earth
Ephemerides at 1 epochs from 2020-04-29 10:44:09.186 (TDB) to 2020-04-29 10:44:09.186 (TDB)
This does not require any external download. If on the other hand you want to use higher precision ephemerides, you can tell Astropy to do so:
>>> from astropy.coordinates import solar_system_ephemeris
>>> solar_system_ephemeris.set("jpl")
Downloading http://naif.jpl.nasa.gov/pub/naif/generic_kernels/spk/planets/de430.bsp
|==========>-------------------------------| 23M/119M (19.54%) ETA 59s22ss23
This in turn will download the ephemerides files from NASA and use them for future computations. For more information, check out Astropy documentation on ephemerides.
If you want to retrieve the osculating orbit at a given epoch, you can do so using from_ephem():
>>> Orbit.from_ephem(Sun, earth, epoch)
1 x 1 AU x 23.4 deg (HCRS) orbit around Sun (☉) at epoch 2020-04-29 10:43:00.000 (UTC)
Note
Notice that the position and velocity vectors are given with respect to the Heliocentric Celestial Reference System (HCRS) which means equatorial coordinates centered on the Sun.
In addition, hapsira supports fetching orbital information from 2 online databases: Small Body Database Browser (SBDB) and JPL HORIZONS.
HORIZONS can be used to generate ephemerides for solar-system bodies, while SBDB provides model orbits for all known asteroids and many comets. The data is fetched using the wrappers to these services provided by astroquery:
epoch = Time("2020-04-29 10:43")
ephem_ceres = Ephem.from_horizons("Ceres", epoch)
orbit_apophis = Orbit.from_sbdb("Apophis")
Traveling through space: solving the Lambert problem¶
The determination of an orbit given two position vectors and the time of flight is known in celestial mechanics as Lambert’s problem, also known as the two body boundary value problem. This contrasts with Kepler’s problem or propagation, which is rather an initial value problem.
hapsira allows you to solve Lambert’s problem by passing the initial and final orbits to hapsira.maneuver.Maneuver.lambert() instance. The time of flight is computed internally since orbits epochs are known.
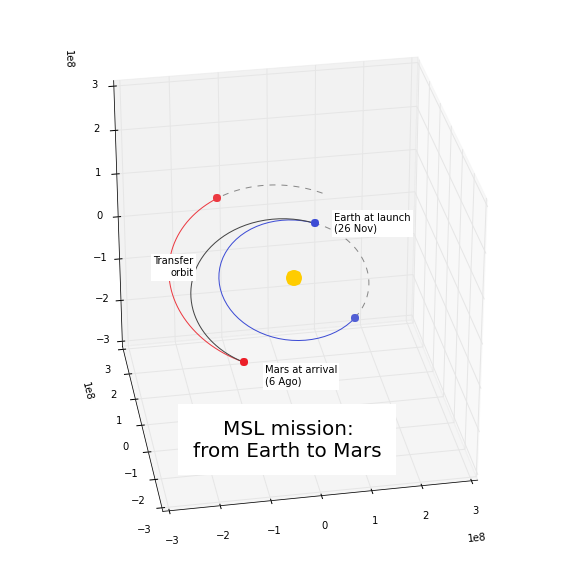
For instance, this is a simplified version of the example “Going to Mars with Python using hapsira”, where the orbit of the Mars Science Laboratory mission (rover Curiosity) is determined:
date_launch = Time('2011-11-26 15:02', scale='tdb')
date_arrival = Time('2012-08-06 05:17', scale='tdb')
orb0 = Orbit.from_ephem(Sun, Ephem.from_body(Earth, date_launch), date_launch)
orbf = Orbit.from_ephem(Sun, Ephem.from_body(Mars, date_arrival), date_arrival)
man_lambert = Maneuver.lambert(orb0, orbf)
dv_a, dv_b = man_lambert.impulses
And these are the results:
>>> dv_a
(<Quantity 0. s>, <Quantity [-2.06420561, 2.58796837, 0.23911543] km / s>)
>>> dv_b
(<Quantity 21910501.00019529 s>, <Quantity [287832.91384349, 58935.96079319, -94156.93383463] km / s>)
Creating a CZML document¶
You can create CZML documents which can then be visualized with the help of Cesium.
First, load the orbital data and the CZML Extractor:
from hapsira.examples import molniya, iss
from hapsira.czml.extract_czml import CZMLExtractor
Then, specify the starting and ending epoch, as well as the number of sample points (the higher the number, the more accurate the trajectory):
start_epoch = iss.epoch
end_epoch = iss.epoch + molniya.period
sample_points = 10
extractor = CZMLExtractor(start_epoch, end_epoch, sample_points)
extractor.add_orbit(molniya, label_text="Molniya")
extractor.add_orbit(iss, label_text="ISS")
Finaly, generate the CZML file by calling extractor.packets. There is more information in this sample Cesium application.
Per Python ad astra ;)